Research
Feb 7, 2017Hidden in Plain Sight: Transacting Privately on a Blockchain
Introducing Confidential Assets in the Chain Protocol
A blockchain works because all participants can validate every transaction. In order to do this, those transactions must be broadcast to the entire network. Unfortunately, this leaks sensitive information, making a blockchain a seemingly poor choice for any market-spanning infrastructure. But what if everyone could validate every transaction without seeing the contents? This is the goal of cutting edge R&D at Chain and in the blockchain field more broadly.
In this article we examine the current state of blockchain privacy and introduce Chain’s confidentiality work, called Confidential Assets, which builds upon and extends Gregory Maxwell’s (and others’) work on Confidential Transactions (CT).
The motivation for Chain’s Confidential Assets scheme is to hide not only the amounts in a transaction (as in CT), but also the asset types. In contrast to networks like Bitcoin that only have one asset circulating, and thus do not have to worry about this problem, Chain-enabled networks typically contain many different asset types, such as several different currencies and securities. We do not want other network participants to know which assets are being traded, or in what volume, but still want them to be able to verify that the transactions are valid. This is the problem Confidential Assets solves.
In addition, the scheme enables both confidential and non-confidential assets to co-exist on a single blockchain and allows for selective disclosure of private data to designated third parties. It makes privacy a native feature of Chain’s data model and architecture, not an add-on or special out-of-band case. It is compatible with blockchain programs (see: Ivy) and relies on established cryptographic primitives that allow us to optimize for performance and scalability.
The Current State of Blockchain Privacy
The problem of financial privacy on blockchains was first formulated by Satoshi Nakamoto in the Bitcoin whitepaper in 2008:
The traditional banking model achieves a level of privacy by limiting access to information to the parties involved and the trusted third party. The necessity to announce all transactions publicly precludes this method, but privacy can still be maintained by breaking the flow of information in another place: by keeping public keys anonymous.
To preserve some degree of privacy on the Bitcoin blockchain, users adopted so-called “one-time keys,” which became ubiquitous thanks to Pieter Wuille’s protocol for “hierarchical deterministic wallets” (BIP 32). This approach has been adopted by a variety of blockchain solutions, including the Chain Protocol.
However, this only partially obfuscates the transaction history. The blockchain still reveals the amounts being transferred, as well as the links between one transfer of value and the next transfer of that value. In other words, one-time keys provide privacy of identity, but do not address privacy of amounts and privacy of history. Moreover, observers can use patterns in the remaining data to de-anonymize and trace the history of certain transfers on the chain, compromising even the privacy of identity. Thus, it’s necessary to go further.
Privacy of amounts
Gregory Maxwell, Andrew Poelstra, Adam Back, and others at Blockstream developed “Confidential Transactions,” a protocol for encrypting the input and output amounts of a transaction in a way that still allows the network to validate that the transaction balances. Notably, the confidential transactions scheme does not depend (at least in theory) on any cryptographic assumptions other than those used for the elliptic curve digital signatures that are already used in Bitcoin and other blockchain protocols.
Currently, Confidential Transactions is implemented as part of Blockstream’s Elements Alpha sidechain. A version of it, called RingCT, is implemented by the Monero project.
Privacy of transaction history
Another concern about on-blockchain privacy is that the inputs used in a transaction can be traced to the previous transactions that created them. This can reveal sensitive information about transfers. Protocols such as CoinJoin, TumbleBit, MimbleWimble, CryptoNote (a version of which is implemented in Monero) and Zerocash (implemented in Zcash) take various approaches to solving this problem.
Chain’s approach to privacy
In contrast to Bitcoin, Monero and Zcash, which only support a single asset (BTC, XMR, and ZEC, respectively), the Chain Protocol — our shared ledger protocol designed for enterprise financial infrastructure — supports multiple types of assets on the same network.
Therefore, to achieve asset privacy in the Chain Protocol, both the amounts and asset types must be kept confidential. This is the primary focus of our work on Confidential Assets. It does not yet directly address history privacy, which is an area of active research for us.
Before diving into the technical details of how each are made confidential, let’s look at an overview of the constituent parts.
Confidential transfer
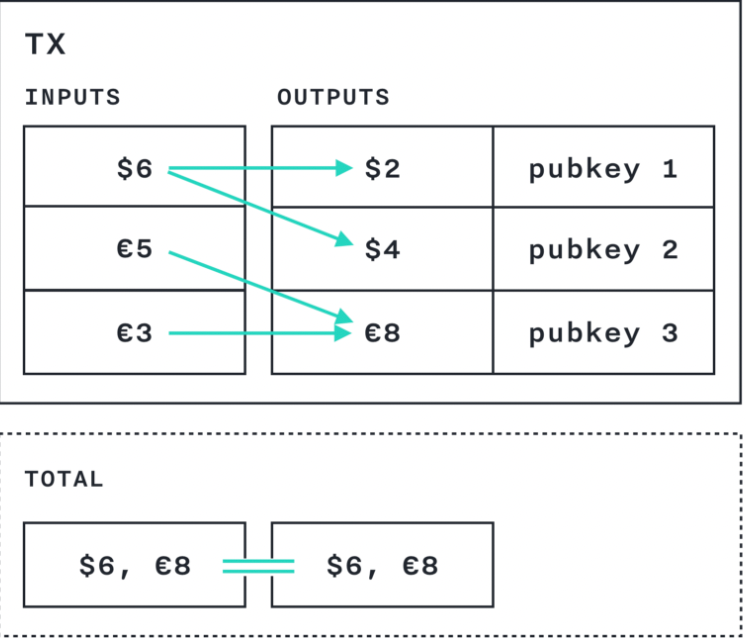
In the Chain Protocol, value is transferred using data structures called “transactions:”

Broadly speaking, the inputs in a transaction specify the sources of value for the transaction; the outputs specify the destinations for that value. The integrity of the ledger depends on the inputs and the outputs in a given transaction balancing.
Confidential Assets allows anyone to ensure that a transaction balances without seeing the amounts and asset identifiers.
Amounts and/or asset identifiers may be publicly revealed on the blockchain (which may be necessary for smart contract validation) or privately unblinded to designated third parties by sharing one-time blinding keys.
Confidential issuance
Transactions in the Chain Protocol can also include “issuance inputs” that generate new units of an asset. An issuance must satisfy the “issuance program” of that asset (which could involve a signature corresponding to a given public key).
With Confidential Assets, units of an asset can also can be issued without revealing the amount or asset ID of the issuance input.
Confidential Assets: Under the Hood
In this section, we present the current design of Confidential Assets as implemented in our forthcoming version of Chain Core. In a separate article, we will discuss further improvements to the scheme that are still in progress.
We need to make asset amounts and identifiers private, which requires some form of encryption. At the same time, anyone should be able to verify that the transaction is balanced — i.e., that no new units of any asset are created without authorization. If the outputs of a transaction contain 10 units of a given asset, the inputs must contain exactly 10 units of that asset. Asset types should not be allowed to “morph” into each other, and new units should not be created or destroyed in the transaction (other than through retirement or authorized issuance).
Traditional permutation-based encryption schemes will not help us because, by design, they obfuscate all structure of the encrypted data, making it impossible for a verifier to determine whether the encrypted transaction is valid. Instead, we need some form of homomorphic encryption designed specifically to provide a zero-knowledge proof that the transaction is balanced. Our building blocks will be arithmetic on the elliptic curve (in our case, Curve25519) and the difficulty of the “elliptic curve discrete logarithm problem” (ECDLP).
We start with mapping each asset identifier to a point on the elliptic curve:
USD -> point A
EUR -> point B
...
An amount of any asset type is represented as that asset ID multiplied by a scalar:
10 USD -> point 10·A
11 EUR -> point 11·B
...
Transaction outputs have to specify these points instead of the cleartext asset identifiers and amounts. Points that represent asset identifiers (A, B, …) must be chosen in such a way that no one knows the discrete logarithm of any point with respect to any other point; for instance, by hashing each asset ID to a point on a curve. We refer to such points as “orthogonal” with respect to one another.
Orthogonal asset ID points make it computationally hard to “morph” one asset into another: that is, claiming that 55·C of some other asset type C is actually 5·A. If this property holds, then the only way to construct a valid transaction will be to balance the units of each asset independently:
Inputs Outputs
6·A 2·A
5·B 4·A
3·B 8·BTotal
6·A + 8·B == 6·A + 8·B
Mapping amounts and asset identifiers in this way does not by itself provide privacy, since it is easy to enumerate likely values and check if they match the published points. To make amounts truly private, we need to introduce blinding factors.
Blinded commitments
In this example, we will create a blinded commitment to v units of an asset A (where v is a positive integer and A is an elliptic curve point that corresponds to an asset ID).
First, we obfuscate the asset identifier using a Pedersen commitment:
H = A + c·G
G is another point, orthogonal to all asset identifier points (meaning, that discrete logarithm of G with respect to any asset ID point is unknown). For simplicity, we use the standard base point on Curve25519. The scalar c is a randomly selected integer that acts as “noise,” making it computationally impossible to guess which asset identifier is being hidden.
Next, we multiply the amount v by the blinded asset identifier H and add its own blinding factor f using another Pedersen commitment:
V = v·H + f·G
We define the point V to be a blinded value commitment. If we expand H in V (and isolate the non-blinded asset value v·A) we will see that the total blinding factor is v·c + f.
Each transaction output includes a commitment V. When the sum of the input value commitments is compared with the sum of the output value commitments, the orthogonality of all asset points A, B etc. (between each other and with respect to the base point G) guarantees that all amounts are balanced for each asset type and all blinding factors are balanced by themselves without affecting the amounts.
With the tools above we can blind asset identifiers on outputs, unlinking them from asset identifiers on the inputs, and also fully blind the amounts. However, without additional proofs, that scheme is insecure. Since the group defined on the elliptic curve is cyclic, it is possible for a blinded value commitment to commit to a “negative” amount, meaning slightly less than the order of the finite group defined by Curve25519. When such a “negative” output is added with another output with an extra amount, the total value could overflow the group order and balance with the inputs, producing extra units of a given asset type without explicit and authorized issuance.
Maxwell describes this problem in his summary of his Confidential Transactions scheme, and proposes a solution, value range proofs, which we adapted for our own scheme, as described below. Value range proofs prove that a value commitment contains no more than 2^N units of an asset.
However, multi-asset confidentiality adds an additional wrinkle. Value range proofs can only prove that a value contains a limited amount of an asset with respect to a specific generator (or, in our case, asset ID). Since in confidential transactions, the asset ID is blinded, a malicious party could use an asset ID corresponding to, essentially, –1·A, for some target asset A. This would allow them to construct a valid value range proof for a value commitment that contains a “negative” amount of asset A, and thus allow them to create extra units in another output, as described above.
To prevent this, we require an additional range proof for each output: an asset range proof.
Asset range proofs
The asset range proof proves that the asset ID commitment on each output is a blinded version of one of the asset ID commitments on the inputs.
Verifiers construct a set of public keys by subtracting each input commitment (H1, H2, …) from the given output commitment (H′):
P1 = H′ — H1
P2 = H′ — H2
...
Pn = H′ — Hn
If H′ indeed commits to the same asset ID as one of H1, H2, etc, then one of the resulting public keys will be a valid public key with the base point G and a secret scalar equal to the difference between the output blinding factor and one of the input’s blinding factors. That is, the asset identifier will be cancelled out.
Pi = (A + c′·G) — (A + c·G)
= (c′ — c)·G
This means that the party can create a Schnorr signature using (c′ — c) as the private key, (H′ — Hi) as the public key, and G as the generator. That signature serves as a proof of knowledge of the discrete log, which in turn proves that H′ and Hi commit to the same asset identifier.
If there is no corresponding input that commits to the same output, then each of the keys in the ring signature will include terms that cannot be easily factored out.
Hj = B + c·G
H′ = A + c′·G
Pj = A — B + (c′ - c)·G
Since all points representing asset identifiers are orthogonal with respect to each other and G, it is computationally hard to figure out a secret scalar with respect to G to sign for Pj.
To actually hide the link between an input asset ID commitment and an output commitment, we need a ring signature. A ring signature is a relatively simple extension of a Schnorr signature to multiple public keys that can be created with knowledge of just one of the corresponding private keys. The verifier will not be able to tell which one of the keys was used for signing. The scheme uses the same assumptions about ECDLP and collision-resistant hash functions as regular EdDSA signatures.
Once H′ is proven to have a “good form” by a ring signature, we can use that asset ID commitment as the basis for our value range proof.
Value range proofs
To prove that the value commitment does not commit to a “negative” amount of the given asset, we need a proof that the number is in a range of allowed values. The Chain Protocol uses 64-bit integers, which are sufficiently large to be useful, but small enough so that the sum of all output values cannot overflow the curve’s order (≈252 bits).
The simplest proof would be a ring signature that enumerates all possible values from 0 to 2⁶⁴–1, subtracting them from the value commitment to produce a public key for each possible value:
P0 = V — 0·H
P1 = V — 1·H
...
Pn = V – 18446744073709551615·H
A ring signature over this range of keys would prove that the value commitment was a blinded commitment to one of those values. Unfortunately, such a ring signature would take an impossible amount of memory and CPU to create and verify.
To make it efficient, Gregory Maxwell in his work on CT suggested encoding the value using distinct encrypted digits. Each digit would be represented as its own commitment to a narrower range of values, and the total value commitment would be reconstructed from the sum of all digit commitments.
For example, a range proof for the value commitment V = 292·H + f·G could use three base-10 digit commitments:
D2 = 200·H + f1·G
D1 = 90·H + f2·G
D0 = 2·H + f3·G
If f1, f2, and f3 are chosen to add up to f, then D0, D1, and D2 will together sum up to V. The prover therefore only needs to prove that these values are low enough that their sum must be in range.
D2 can be proven to be in range with a ring signature where 10 public keys are formed by subtracting 0·H, 100·H, 200·H,… 900·H from V. The range proof for D1 can subtract 0·H, 10·H, 20·H,… 90·H from V, and the range proof for D0 can subtract 0·H, 1·H, 2·H,… 9·H from V. It is easy to see that a 64-bit number would require 20 decimal digits, each having only 10 signatures — a total of 200 signatures, which is significantly less than enumerating all 64-bit values one by one!
The CT scheme goes further in optimizing bandwidth and CPU costs. All per-digit ring signatures are cleverly connected together in a Borromean Ring Signature construction that additionally saves 32 bytes per digit. With this construction, the optimal base for digit commitments turns out to be 4. We implemented these useful optimizations in Chain’s value range proofs as well.
As a result, 64-bit numbers can be represented using approximately 5Kb of data, consisting mostly of value range proofs. Validating a value range proof requires up to 128 signature checks. Asset range proofs are proportional in size to the number of inputs and take only a small part of the total overhead (up to N signature checks per output, where N is the number of inputs).
Conversion
Outputs in a transaction can be selectively blinded and unblinded. Non-confidential inputs can be transferred into confidential outputs, and vice versa.
To balance a transaction that includes both confidential and non-confidential values, verifiers can construct unblinded commitments to the asset ID and amount, which can be used when balancing the transaction:
A = HashToPoint(assetID)
H = A
V = amount·H
Confidential issuance
We have shown how transfers are handled in our scheme, but have not yet addressed the question of where this value originally comes from. Some inputs spend previous outputs, unlocking the value stored in those outputs. Other inputs are issuances that introduce new units of any asset to the system. Confidential Assets support both public issuance and confidential issuance.
In the Chain Protocol, an asset identifier is a hash of the issuance program — the program that must be satisfied for an asset to be issued. (This idea is inspired by the OpenAssets protocol proposed by Flavien Charlon.) An “issuance input” can contain an arbitrary asset ID and amount, but in order to be valid, it must satisfy the corresponding issuance program. Issuance programs can range from simple multi-signature programs to more elaborate conditions that put restrictions on the amount or frequency of issuance, or impose additional requirements such as retirement of some other asset.
If we want to obfuscate the asset ID being issued, we can do so using an issuance asset range proof.
Every asset identifier can be associated with an issuance public key. It is an ordinary public key necessary to authorize issuance in a confidential manner:
Y = y·G
A confidential issuance input declares a blinded asset ID commitment, just like an output:
H = A + c·G
The issuer declares a set of cleartext asset ID candidates and uses a ring signature to prove that H commits to one of them. The ring signature is constructed with an addition of the issuance public key to make it impossible to commit to any given asset ID without knowing its issuance private key.
Candidate asset ID points:
A1, A2, … AnCorresponding issuance public keys:
Y1, Y2, … Yn
Each public key in the ring signature subtracts a corresponding asset ID candidate:
P1 = H — A1 + h·Y1
P2 = H — A2 + h·Y2
...
Pn = H — An + h·Yn
where h is a hash of the blinded asset commitment H. This is effectively a trick that uses a Fiat-Shamir transform to make sure that H cannot be constructed to cancel out someone’s issuance key and commit to their asset ID. If H actually commits to one of the asset IDs, then the corresponding public key has that asset ID cancelled out:
Pi = (Ai + c·G) — Ai + h·Yi
Pi = (c + h·y)·G
where y is the issuance private key for asset Ai. Since the blinding factor c is determined before h is known (due to a one-way hash), it is infeasible to cancel out that issuance key. Therefore, the knowledge of both the blinding factor and the issuance key is necessary to construct a valid issuance asset range proof: the signing private key would be c + h·y.
Once the blinded asset ID commitment H is proven to be valid, the value can be blinded based on it in the same manner as in any output, with a blinded commitment and an associated multi-digit range proof as discussed above:
V = v·H + f·G
The remaining question is how to associate these issuance keys with the asset identifiers.
Uniform Asset Identifiers
In the candidates list, we declare a set of asset IDs together with issuance keys. Each asset ID’s issuance program must be fully satisfied. This way, each issuer may declare an issuance key that may be used to issue that asset confidentially. The issuance programs may optionally access the corresponding issuance key and verify that it matches the built-in, or pre-signed, value.
The Chain Virtual Machine (Chain VM) includes a special instruction, ISSUANCEKEY, that, when used in the context of a confidential issuance, returns the corresponding issuance key. It allows an issuer to create an asset ID that delegates issuance to that key — or, more precisely, to a ring signature that includes that key in the corresponding position:
<pubkey> ISSUANCEKEY EQUAL
Anyone can satisfy this issuance program provided they do so in a confidential issuance input that uses the same issuance public key. The issuance range proof will prevent issuers from claiming issuance of asset IDs for which they do not know the corresponding issuance private key.
Finally, the issuance asset range proof needs to commit to the specific transaction that is authorized. It therefore signs an issuance delegate program chosen by the creator of the transaction and declared in the issuance input. After the proof is checked, the program is evaluated. The program can, in turn, commit to the transaction hash (or any other specific part of the transaction).
Conclusion
We have presented a confidentiality framework, Confidential Assets, that dramatically improves financial privacy on a blockchain network in a scalable and integrated manner. The solution is based on time-tested cryptographic assumptions, its implementation is minimally complex, and integration with issuance and control programs provides a smooth user experience and a solid foundation for future improvements.
Our multi-asset confidentiality scheme hides asset identifiers and amounts for all transactions, allows unblinding to the whole network or to a specific party, integrates well with blockchain programs, and enables confidential and non-confidential issuance. The scheme is based on Pedersen commitments and provides unconditional privacy and computational binding.
In our next article, we will discuss further security and usability improvements to this protocol that are in development.
Acknowledgements
We would like to thank Dan Boneh, Joseph Bonneau, Gregory Maxwell, Trevor Perrin and Andrew Poelstra for inspiring conversations about cryptography and blockchain privacy that contributed greatly to the development of Confidential Assets.
Chain News & Updates
Latest News & Updates
Sign up for the Chain Newsletter - a weekly roundup of new platform features and the latest from the industry.
